이번에는 저번에 예고한 평균 제곱근 오차 내용부터 시작하겠습니다.
저번 글 내용에서는 최소 제곱법 공식을 이용하여 직선을 그렸지만 이 공식은 변수를 하나만 갖는 다는 단점이 있습니다. 실제로 딥러닝을 적용할 때는 한 가지보다는 다중의 조건이 많으며 이를 고려하기 위해 좀 더 복잡한 연산 과정이 필요하게 됩니다. 또한, 선을 그린 후 잘 그려졌는지 평가하여 조금씩 수정해가는 오차 평가 알고리즘이 필요합니다.
그렇기 때문에, 오차를 평가하는 방법 중 가장 많이 사용되는 평균 제곱근 오차에 대해 공부해보겠습니다.
해당 방법에 대해 쉽게 설명하자면, 일단 그리고 조금씩 수정해나가는 방식입니다. 기존에는 최소 제곱법을 이용하여 a, b를 구했지만 이번에는 임의 a, b를 입력해보겠습니다. 그 다음 주어진 x, y를 대입한 후 오차가 얼마 나는지 확인하기 위해 각 점과 그래프 사이의 거리를 측정합니다.
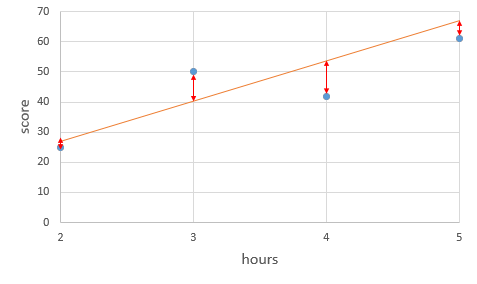
위 그림에서 볼 수 있는 빨간색 선은 직선이 잘 그어졌는지를 나타내는데 이 직선들의 합이 작을 수록 잘 그어진 것을 의미하며 합이 클수록 잘못 그어진 것을 의미합니다.
오차를 구하는 방식은 : 오차 = 실제값 - 예측값
(예 : 공부한 시간 2 / 성적 81 / 현재 식에 대입해서 나온 예측값 85 / 오차 3) 이지만 이렇게 차를 이용하여 모든 값을 더할 경우 음수와 양수가 섞여서 합이 0이 될 수 있기 때문에 오차 값의 제곱을 해서 더해야 정확한 오차 정도를 알 수 있습니다.

위에 보시다싶이 i는 x가 나오는 순서를 n은 x 원소의 총 개수를 의미합니다. 첫번째 있는 y 값은 x 값에 대한 실제 값이고 두 번째 있는 y 값은 x가 대입되었을 때의 직선의 방정식이 만드는 예측값입니다. (예 : 공부한 시간 2 / 성적 81 / 현재 식에 대입해서 나온 예측값 85 / 오차 제곱 9) (9+2+1+5=17)
이렇게 모든 예측값을 더하고 x 값의 평균 오차를 이용합니다. 위에 구한 값을 n으로 나누면 오차 합의 평균을 구할 수 있는데 이가 평균 제곱 오차입니다. (예 : 17/4=4.2)
이때, 평균 제곱 오차가 너무 커서 쓰기가 불편한 때가 있는데 이를 방지하기 위해 제곱한 숫자에 다시 제곱근을 씌워줍니다. 이를 평균 제곱근 오차라고 합니다. (4.2 에 제곱근 2) 이렇게 구했다면 다음에 하는 일은 평균 제곱근 오차 계산 결과가 가장 작은 선을 찾는 작업이라고 할 수 있습니다.
선형 회귀란?
임의의 직선을 그어 이에 대한 평균 제곱근 오차를 구하고, 이 값을 가장 작게 만들어주는 a와 b 값을 찾아가는 작업입니다.
이제 평균 제곱근 오차를 파이썬으로 구현해보겠습니다.
1. 다음 코드에서 사용할 함수들을 사용하기 위해 라이브러리 추가
import numpy as np
2. 임의로 정한 기울기 a, b 값을 정해줍니다.
- 이 임의로 정한 기울기를 통해 평균 제곱근 오차(Root mean squared error, RMSE)를 구하게 됩니다. 이 rmse 값이 클수록 오차가 크다는 뜻은 a, b가 올바르지 않다는 것을 뜻하게 됩니다.
#임의로 정한 기울기 a와 b
ab = [3,89]
3. x, y의 데이터 값으로 [공부한 시간, 시간에 따른 성적 결과]를 뜻합니다.
# x, y 데이터 값
data = [[2, 56], [5, 67], [8, 88], [11, 81], [14, 91]]
x = [i[0] for i in data]
y = [i[1] for i in data]
4. predict 함수를 구현하여 y = ax + b 식을 구현해줍니다.
# y = ax + b
def predict(x):
return ab[0]*x + ab[1]
5. 그 다음은 제곱근 공식을 함수로 옮긴 코드입니다.
np.sqrt()은 제곱근을 **2 제곱을 구하라는 뜻이며 mean()은 평균값을 구하라는 뜻입니다. 예측값과 실제 값을 각각 rmse 함수의 p와 a 자리에 입력해서 평균 제곱근을 구합니다.
# rmse 함수
def rmse(p, a):
return np.sqrt(((p-a)**2).mean())
6. rmse 함수를 각 y 값에 대입하여 최종 값을 구하는 함수
# rmse 함수를 각 y 값에 대입하여 최종 값을 구하는 함수
def rmse_val(predict_result, y):
return rmse(np.array(predict_result), np.array(y))
7. 마지막으로 결과를 출력해주는 코드
# 예측 값 들어갈 빈 리스트
predict_result = []
#모든 x 값을 한번 씩 대입
for i in range(len(x)):
predict_result.append(predict(x[i]))
print("공부하는 시간 =%.f, 실제 점수 =%.f 예측점수 =%.f" % (x[i],y[i],predict(x[i])))
#최종 rmse 출력
print("rmse 최종 값 : " + str(rmse_val(predict_result, y)))
- 여기 predict_result.append(predict(x[i])) 에서는 x 값을 대입했을 때의 예측값이 저장된다.
- rmse_val(predict_result, y)) 에서는 예측값과 실제값이 들어가서 다시 np.array(predict_result),np.array(predict_result) 로 들어가 np.sqrt(((p-a)**2).mean()) 이곳에서 계산이 되는데 예측값 - 실제 값을 해서 제곱한 후에 다 더한 후 평균을 구해서 다시 루트를 씌워 결과를 내게 된다.
결과 :

최종적으로 임의의 a, b를 정해서 테스트 해보았을 때의 실제 점수와 예측 점수가 위처럼 나오고 이에 대한 오차를 정리한 결과 36 정도가 난다는 것을 알 수 있기 때문에 a, b의 오차가 크고 잘못 설정되었다는 것을 알 수 있다.
전체 코드 :
import numpy as np
#임의로 정한 기울기 a와 b
ab = [3,89]
# x, y 데이터 값
data = [[2, 56], [5, 67], [8, 88], [11, 81], [14, 91]]
x = [i[0] for i in data]
y = [i[1] for i in data]
# y = ax + b
def predict(x):
return ab[0]*x + ab[1]
# rmse 함수
def rmse(p, a):
return np.sqrt(((p-a)**2).mean())
# rmse 함수를 각 y 값에 대입하여 최종 값을 구하는 함수
def rmse_val(predict_result, y):
return rmse(np.array(predict_result), np.array(y))
# 예측 값 들어갈 빈 리스트
predict_result = []
#모든 x 값을 한번 씩 대입
for i in range(len(x)):
predict_result.append(predict(x[i]))
print("공부하는 시간 =%.f, 실제 점수 =%.f 예측점수 =%.f" % (x[i],y[i],predict(x[i])))
#최종 rmse 출력
print("rmse 최종 값 : " + str(rmse_val(predict_result, y)))
여기까지 a, b를 임의로 설정하였을 때 이 a, b가 실제 정답에 가까울지 가깝지 않을지 판별하는 과정을 평균 제곱근 오차 계산을 통해서 알아내었다. 다음은 정답에 가깝지 않을 때, 어떻게 a, b의 값을 조정해서 정답에 가깝게 만들지에 대해 공부하고자 한다.
a, b의 값을 조정해서 정답에 가깝게 만들지에 대한 방법 : 경사 하강법
'IT' 카테고리의 다른 글
| [메타버스] 메타버스 마케팅 사례 및 문제점 관련 글 정리 (0) | 2021.08.12 |
|---|---|
| [모두의 딥러닝] 딥러닝 공부 4일차 - 경사 하강법 이론 (0) | 2021.04.02 |
| [모두의 딥러닝] 딥러닝 공부 2일차 - 선형회귀란 / 일차함수그래프 / 최소 제곱근 공식 / 최소 제곱근 활용 코딩 (0) | 2021.03.22 |
| [모두의 딥러닝] 딥러닝 공부 1일차 - 머신러닝이란? 기존 프로그래밍과 차이점 / 딥러닝 코드 분석 (0) | 2021.03.21 |
| [유니티] 스크립트로 텍스트 파일 생성 및 쓰기, 저장 / 파일 입출력 (0) | 2021.02.14 |




댓글