이번 문제는 기존에 풀던 게임 문제집이 아닌 다이나믹 프로래밍 알고리즘으로 넘어와서 문제를 풀게 되었습니다. 저번에 풀면서 느꼈지만 DP는 아직 DFS나 BFS만큼 이해가 너무 안되어 있는 거 같아 한동안 지속해서 관련 문제를 풀 필요성을 느끼게 되었습니다.
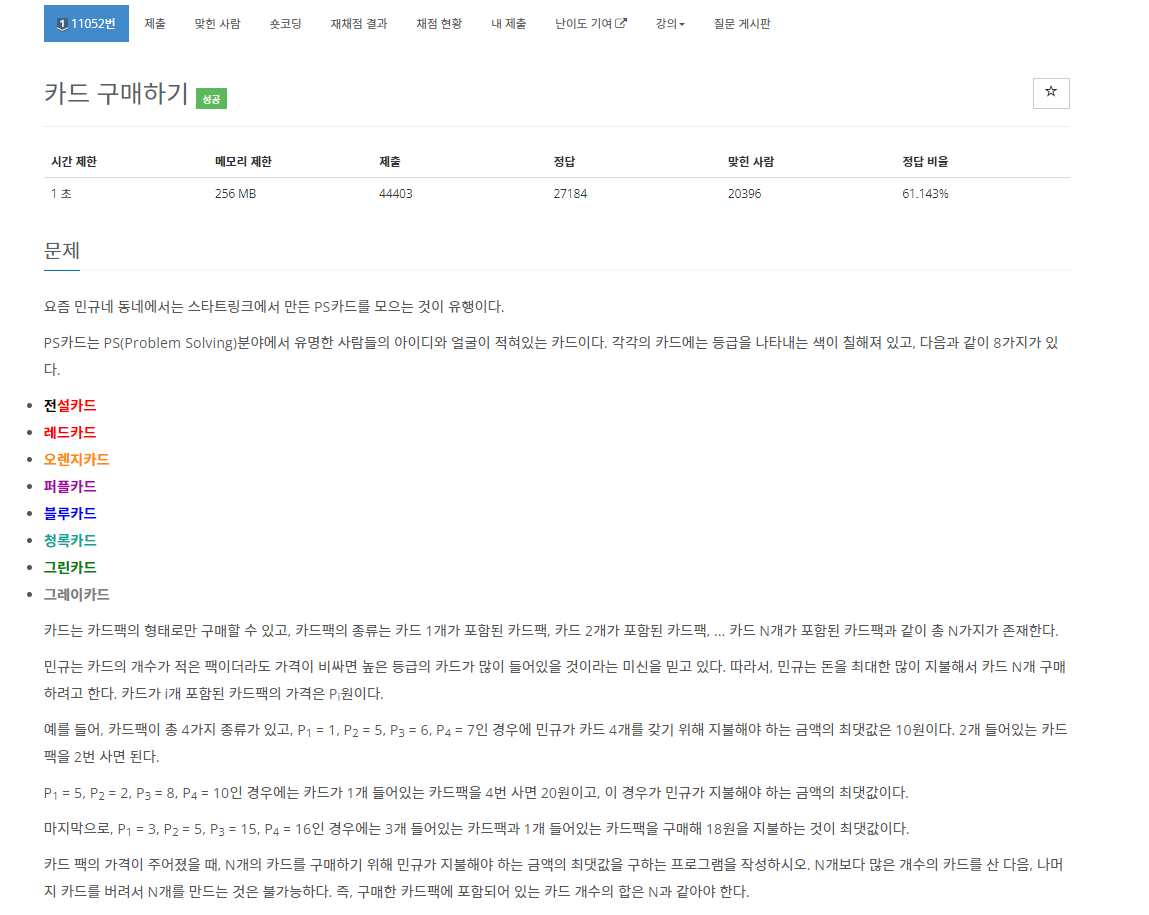
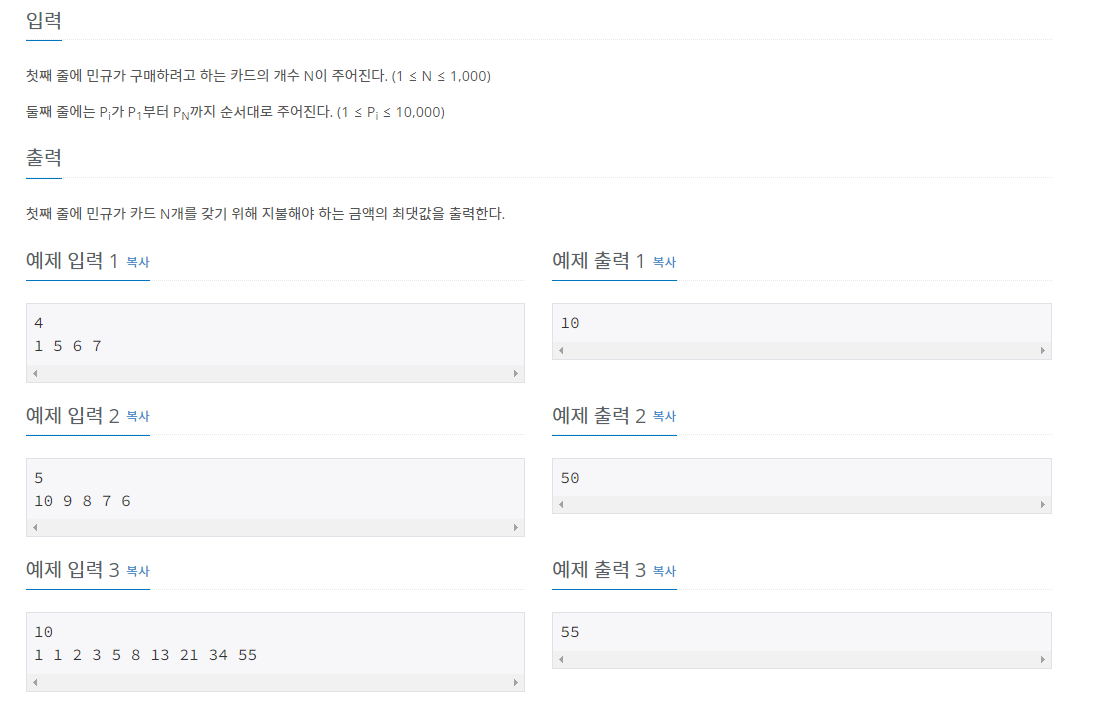
해당 문제는 카드 팩의 가격이 주어졌을 때, N개의 카드를 구매하기 위해 민규가 지불해야 하는 금액의 최댓값을 구하는 프로그램으로 DP에 어떤 값을 누적시킬 건지 중요한 문제인 것 같습니다.
처음에 고민했던 방향은
1. dp 의 i 번째마다 비교하여 i 장 카드 최댓값 넣기
2. dp 의 i 번째마다 비교하여 n 장 카드 최댓값 넣기
였는데 아무래도 dp 값을 활용하는 특징상 후자는 아닌 것 같아 전자로 잡고 문제를 풀게 되었습니다.
아쉽게도 아직 잘 이해되지 않아서 30분동안 고민하다가 안되어서 다른 분의 풀이를 참고해서 풀게 되었습니다. 그리고 제가 이해한 풀이 방법은 다음과 같습니다.
dp 의 i 번째마다 i 장 카드 최댓값 넣는다고 했을 때,
dp[1] = n_list[1]
dp[2] = n_list[2] + dp[0] or n_list[1] + dp[1]
dp[3] = n_list[3] + dp[0] or n_list[2] + dp[1] or n_list[1] + dp[2]
으로 나타낼 수 있고 이는 즉, dp[k] = n_list[i] + dp[k-i] (i = 1, 2, 3) 으로 정의할 수 있다는 점입니다.
큰 값을 비교하기 위해서는 완전 탐색이 필요했고 위의 식을 이용해 다음과 같은 코드로 통과하였습니다.
import sys
input = sys.stdin.readline
n = int(input())
n_list = [0] + list(map(int, input().split()))
dp = [0] * (n+1)
# dp 의 i 번째마다 i 장 카드 최댓값 넣기
# dp[1] = n_list[1]
# dp[2] = n_list[2] + dp[0] or n_list[1] + dp[1]
# dp[3] = n_list[3] + dp[0] or n_list[2] + dp[1] or n_list[1] + dp[2]
# dp[k] = n_list[i] + dp[k-i] i = 1, 2, 3
for i in range(1, n+1):
for j in range(1, i+1):
dp[i] = max(n_list[j] + dp[i-j], dp[i])
print(dp[n])
다이나믹 프로그래밍 문제를 풀기 위해서는 규칙성을 찾고 식을 세우는 것이 매우 중요한 것 같습니다.
'알고리즘' 카테고리의 다른 글
| [알고리즘/백준] 2193번 이친수 Python 파이썬 (0) | 2023.04.19 |
|---|---|
| [알고리즘/백준] 11057번 오르막 수 Python 파이썬 (0) | 2023.04.18 |
| [알고리즘/백준] 2294번 동전2 Python 파이썬 (2) | 2023.04.10 |
| [알고리즘/백준] 2045번 마방진 Python 파이썬 (0) | 2023.04.06 |
| [알고리즘/백준] 2021번 최소 환승 Python 파이썬 (0) | 2023.04.05 |




댓글