안녕하세요 오늘 다익스트라 알고리즘에 대한 글을 적어볼까합니다.
원래 저는 알고리즘 공부하는 것을 그렇게 좋아하지 않는데요 왜냐하면 알고리즘을 배워도 게임 개발에 어떻게 써먹어야할지 잘 안 와닿기 때문입니다. 하지만 확실히 개발하다 보면 필요할 때가 오게 됩니다. 그래서 이번에는 제가 어떤 게임을 개발하면서 어떤 부분에 이런 알고리즘 활용해서 기능을 개발할 수 있는 지와 이 알고리즘 방식에 대해 저 나름대로 설명을 풀어나갈까 합니다!

이번에 제가 만든 게임은 어떤 장소에서 순찰하는 적이 있고 그 순찰하는 적을 피해서 플레이어가 아이템을 획득해서 탈출하는 게임입니다. 여기서 중요한 부분은 아무래도 적의 움직임입니다. 적의 움직임이 너무 쉽고 단조롭다면 난이도가 하락하고 플레이어들이 덜 재밌어 하겠죠?

그래서 저 같은 경우, 처음 구상을 플레이어가 적에게 타켓팅 되지 않았을 경우, 맵 내에 돌아다니면서 순찰 -> 플레이어가 타켓팅 될 경우, 플레이어 추적 -> 플레이어가 멀어졌을 경우, 다시 맵 내에 순찰 이런 구조의 움직임을 구상했습니다.
하지만 문제가 맵 내에 무작위하게 좌표를 찍어서 순찰하고자 하니 제가 가진 맵은 중앙에 빈 공간들이 있어서 몬스터가 갈 수 없는 곳들이 많았습니다. 이런 부분들을 다 좌표로 예외처리해주는 거 어렵다고 생각해서 직접 순찰 노선을 만들어주기로 하였습니다.
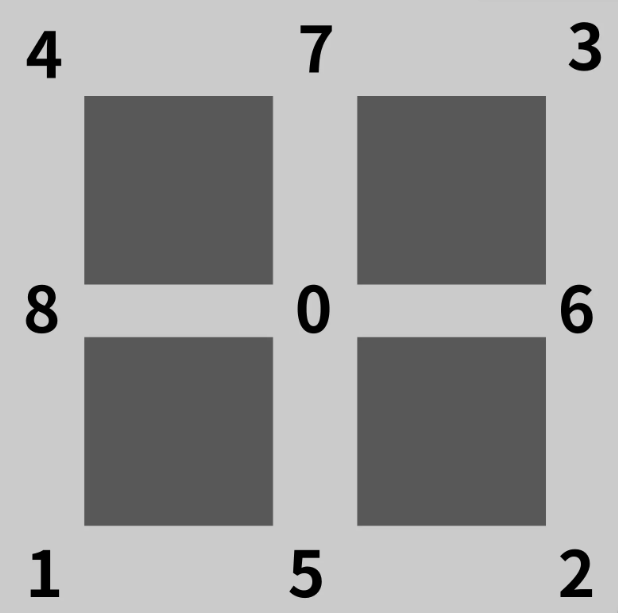
위의 그림은 지도로 제가 개발하던 맵이 위에처럼 생겼고 제가 직접 순찰 지점을 정해서 각 지점에 번호를 붙여줬습니다. 이때 고려한 점은 적을 움직일 때 따로 네비메쉬를 안 쓰고 직전으로 움직이는 단순 움직이기 때문에 이 지점들이 직선으로 이어지게 만들어주었습니다.
그럼, 이제 각 지점에서 갈 수 있는 지점들이 정해지게 됩니다. 이 형태는 바로 그래프 형태가 되는 것이죠!
코드로 구상하면 아래와 같이 만들 수 있게 됩니다.
// 그래프 정의
const graph = {
0: [{node: 8, weight: 1}, {node: 6, weight: 1}, {node: 5, weight: 1}, {node: 7, weight: 1}],
1: [{node: 8, weight: 1}, {node: 5, weight: 1}],
2: [{node: 5, weight: 1}, {node: 6, weight: 1}],
3: [{node: 7, weight: 1}, {node: 6, weight: 1}],
4: [{node: 7, weight: 1}, {node: 8, weight: 1}],
5: [{node: 1, weight: 1}, {node: 0, weight: 1}, {node: 2, weight: 1}],
6: [{node: 0, weight: 1}, {node: 3, weight: 1}, {node: 2, weight: 1}],
7: [{node: 4, weight: 1}, {node: 3, weight: 1}, {node: 0, weight: 1}],
8: [{node: 1, weight: 1}, {node: 4, weight: 1}, {node: 0, weight: 1}],
};
그리고 적을 움직이는 방식에는 1. 현재 지점으로부터 갈 수 있는 지점 중 한 곳을 무작위로 택해서 움직이는 방법과 2. 현재 지점으로부터 아무 지점이나 무작위로 택해서 움직이는 방법이 있습니다. 다만 전자 같은 경우, 코드 짜기는 더 쉬울 수 있으나 그럴 경우, 맵 전체를 돌아다닐 확률이 낮아서 저는 후자 방법을 택하게 되었습니다.
그렇다면 그 다음으로 필요한 기능은 A 지점에서 B지점으로 이동할 때 어떻게 가야할지 길을 찾는 방법일 것입니다.
길 찾기 알고리즘이라고 구글에 치시면 다익스트라 알고리즘과 A* 알고리즘이 제일 많이 뜰 것 입니다. 성능 상 A* 알고리즘이 좋다고 하지만 현재 개발하고 맵 자체가 양수들로 이루어져있고 코드는 다익스트라가 더 직관적이라는 점에서 다익스트라 알고리즘을 골라서 제작하게 되었습니다. 개인적으로 두 가지 다 직접 설계해서 활용해보는 게 좋다고 생각합니다.
다익스트라를 제 방식으로 짧게 설명드리면, 현재 지점을 기점으로 갈 수 있는 지점을 돌면서 현재 몇 번 걸쳐 도착했는가를 지점 별로 반복적으로 기록하면서 가고자 하는 지점의 최단 거리를 찾아가는 방법입니다.
그리고 제 설명이 부실하여 이해가 안되실 분을 위한 실제 정석적인 설명은,
그래프에서 한 정점에서 다른 모든 정점까지의 최단 경로를 찾는 방법입니다. 각 정점 간의 가중치를 고려하며, 시작 정점에서 다른 정점까지의 최소 비용을 계산합니다. 구체적으로, 방문하지 않은 정점 중 최단 거리를 가진 정점을 선택하고, 그 정점에서 갈 수 있는 인접한 정점들의 거리를 업데이트하는 과정을 반복하면서 최단 경로를 찾습니다. 최단 거리를 효율적으로 계산하기 위해 우선순위 큐를 사용하는 것이 일반적입니다.
라고 합니다.
아래는 제가 짠 코드입니다.
dinstance : 시점 지점으로부터 각 지점 별 몇 번 거쳐왔는지 저장하고 비교하는 배열 { 1, 0, 3, 0, 0, 0, 2, 0, 0 } (1번째 지점은 1번만에 갈 수 있음, 3번째 지점은 3번만에 갈 수 있음을 의미)
path : 시작 지점에서 끝 지점으로 향하는 각 지점 별 연결된 최단 지점 { 3, 0, 2, 0, 0, 0, 0, 0, 0 }
visited : 도착 여부 배열 {false, false, false, false, false, false, false, false, false}
queue : 현재 검사해야하는 지점을 담는 배열
.unshift() : 배열의 맨 앞에 값을 추가
.shift() : 배열의 맨 앞에 값을 제거
// 그래프 정의
const graph = {
0: [{node: 8, weight: 1}, {node: 6, weight: 1}, {node: 5, weight: 1}, {node: 7, weight: 1}],
1: [{node: 8, weight: 1}, {node: 5, weight: 1}],
2: [{node: 5, weight: 1}, {node: 6, weight: 1}],
3: [{node: 7, weight: 1}, {node: 6, weight: 1}],
4: [{node: 7, weight: 1}, {node: 8, weight: 1}],
5: [{node: 1, weight: 1}, {node: 0, weight: 1}, {node: 2, weight: 1}],
6: [{node: 0, weight: 1}, {node: 3, weight: 1}, {node: 2, weight: 1}],
7: [{node: 4, weight: 1}, {node: 3, weight: 1}, {node: 0, weight: 1}],
8: [{node: 1, weight: 1}, {node: 4, weight: 1}, {node: 0, weight: 1}],
};
// 다익스트라 알고리즘 함수
function dijkstra(graph, start, end) {
const distances = {}; // 시작 지점으로부터 각 지점 별 몇 번 거쳐왔는지 저장하고 비교하는 배열
const visited = {}; // 도착 여부 배열
const queue = []; // 현재 검사해야하는 지점을 담는 배열
const path = {}; // 시작 지점에서 끝 지점으로 향하는 각 지점 별 연결된 최단 지점
distances[start] = 0; // 시작 지점
queue.push({node: start, weight: 0});
while (queue.length > 0) {
// 가중치 낮은 순으로 검사 -> 한번 검사 노드는 두 번 검사하지 않아서
queue.sort((a, b) => a.weight - b.weight);
const {node, weight} = queue.shift();
if (visited[node]) continue; // 두 번 검사면 패스
visited[node] = true; // 검사 했다 완료 표시
for (const neighbor of graph[node]) { // 갈 수 있는 지점 다 돌기
const newWeight = weight + neighbor.weight; // 가중치 계산
// 기존 가중치 보다 낮거나 아직 정의 되어 있지 않을 경우
if (distances[neighbor.node] === undefined || newWeight < distances[neighbor.node]) {
distances[neighbor.node] = newWeight; // 가중치 업데이트
path[neighbor.node] = node; // 경로 업데이트
queue.push({node: neighbor.node, weight: newWeight});
}
}
}
// 최단 경로 노드 출력
let currentNode = end;
const shortestPathNodes = [end];
while (currentNode !== start) {
currentNode = path[currentNode];
shortestPathNodes.unshift(currentNode);
}
return shortestPathNodes;
}
dijkstra(graph, 1, 7);
해당 위 함수를 귀신의 움직임으로 적용했습니다. 처음 시작할 때, 귀신에게 도착 지점을 무작위로 한 개 정해주고 위의 함수를 통해 최단 거리 노선을 찾아 순차적으로 이동한 게 한 후, 도착 지점에 도착하면 새로운 도착 지점을 다시 설정해주는 방식이었습니다. 그러다가 플레이어를 만나면 쫓아가고 일정 이상 거리가 멀어지면, 제일 가까운 지점을 찾아가서 다시 위에 순찰하는 상태로 바뀌는 거 였습니다.
아 한가지 더 추가한 부분은 도착 지점을 너무 무작위로 주니깐, 정말 운이 좋으면 귀신이랑 동선이 아예 안 겹치는 문제가 있었습니다. 그래서 추가적으로 도착지점을 완전 무작위가 아닌 플레이어와 가까운 4개 지점을 가지고 와서 선택하게 하였더니 확실히 적용 이후, 귀신이 언제 어디서 나타날지 무섭더라고요. 분명 앞 쪽에 있었는데 어느 새 뒤 쪽에 있고....결과적으로 난이도도 올라가고 더 재밌어진 것 같습니다.
아쉬운 점이 있다면, 현재 귀신에게는 2가지 상태가 있는데 순찰 상태, 플레이어 추적 상태 이 부분들을 단순 if 문 처리로 해준 것을 상태 패턴 알고리즘을 사용해서 더 좋은 코드를 만들 수 있지 않았을까 아쉬움이 남는 것 같습니다.
여기까지 긴 글 읽어주셔서 감사합니다.
'알고리즘' 카테고리의 다른 글
| [알고리즘/백준] 1309번 동물원 Python 파이썬 (0) | 2023.04.24 |
|---|---|
| [알고리즘/백준] 11048번 이동하기 Python 파이썬 (1) | 2023.04.21 |
| [알고리즘/백준] 2193번 이친수 Python 파이썬 (0) | 2023.04.19 |
| [알고리즘/백준] 11057번 오르막 수 Python 파이썬 (0) | 2023.04.18 |
| [알고리즘/백준] 11052번 카드 구매하기 Python 파이썬 (1) | 2023.04.12 |




댓글